J'ai réalisé quelques calculs sommaires d'énergétique en partant des
constatations de consommation en fuel et en eau des tracteurs modifiés.
Ceci afin d'essayer de comprendre un peu plus ce qui se passe dans le
réacteur d'un point de vue énergétique.
Nous allons comparer les rendements sur le fuel avant et après la modification.
Ces calculs sont basés sur la réalisation numéro
22, le tracteur Massey Ferguson de 95 CV.
 |
Je considère que le lecteur a bonne connaissance du montage réalisé ( montage Pantone en parallèle de l'injection d'origine, ne traitant que de l'eau, le "gaz" en sortie de réacteur est injecté après le filtre à air). |
Données nécessaires pour comprendre le cheminement :
- 1 CV = 740 W environ
- 1 kWh = 3600 kJ
- Pouvoir calorifique du fuel (environ) : 36 000 kJ/L soit 42 000 kJ/kg soit 1 L de fuel = 10 kWh
- Pouvoir calorifique de l'hydrogène : 120 000 kJ/kg
- Masse molaire de l'hydrogène (H): 1 g/mole
- Masse molaire de l'oxygène (O) : 16 g/mole
- Masse molaire de l'eau (H2O) = 2x1 + 16 = 18 g/mole
- Proportion massique d'hydrogène dans la molécule d'eau : 2/18 = 1/9
Données concernant le tracteur
- Consommation de 21 L/h de fuel en configuration d'origine
- Consommation de 10 L/h de fuel et 6 L/h d'eau après modification
-
Puissance moyenne utile de 70 CV ( approximation basse compte tenu de
la charge de travail qui n'est pas constante et maximale tout le temps)
Hypothèses :
- Nous supposons que le seul produit issu du traitement de l'eau
dans le réacteur est de l'hydrogène. Et nous nous basons sur des
calculs de combustion sommaires (chimiques) en négligeant toutes autres
formes d'apport d'énergie au moteur.
- Soit X la portion massique
d'eau dissociée (dans le réacteur ou dans le moteur) fournissant de
l'énergie sous forme d'hydrogène pour la combustion.
- Soit (1-X) la proportion de vapeur restante qui, surchauffée, fournit de l'énergie en se détendant dans le cylindre.
Nous
raisonnerons sur 1 h de fonctionnement à puissance moyenne de 70 CV,
pour faciliter les calculs, toutes les énergies sont en kWh (1 kWh =
3600 kJ).
Calculs énergétiques :
1) Préliminaire :
Energie utile fournie par le tracteur sur une heure :
E1= puissance du moteur (en Watts) * durée de fonctionnement
= 70*740*3600 = 180 648 kJ = 51.8 kWh
2) Configuration d'origine
Energie thermique fournie par les 21 L de fuel :
E2 = 21*10 = 210 kWh
Rendement global moyen sur le fuel
R1 = E1/E2 = 24.67 %
C'est
le rendement moyen constaté pour les véhicules diesel. Dans notre cas
c'est le rendement que nous appellerons global propre au moteur étudié.
C'est à dire que pour une énergie thermique fournie, ce moteur fournira
environ 25% de cette énergie en énergie mécanique. Cette valeur, compte
tenu de la construction du moteur NE PEUT ETRE DEPASSEE pour augmenter
l'énergie mécanique, il faut augmenter l'énergie thermique fournie.
3) Configuration Pantone
Energie thermique fournie par les 10 L de fuel :E3 = 10*10 = 100 kWh
Rendement global moyen sur le fuel
R2 = E1/E3 = 51.8 %
C'est
énorme! Et cela dépasse le rendement théorique du cycle de Carnot pour
les moteur diesel ( maxi. de environ 40% sur les moteurs diesel
classiques).
Il y a donc de l'énergie qui est fournie par une autre source,
c'est à dire par le gaz sortant du réacteur.
Cette énergie peut provenir de l'eau injectée sous 2 formes :
-
par la combustion de l'hydrogène issu de la décomposition de l'eau, peu
importe que cette décomposition se fasse dans le réacteur ou dans la
chambre de combustion (T et pression élevée) voir 3.1)
- par la détente de la vapeur d'eau qui ne se serait pas décomposée voir 3. 2)
3.1) Etude de l'énergie fournie par la portion X d'eau décomposée.
Sur 1 kilogramme d'eau, nous supposons qu'une quantité X d'eau
est décomposée. En prenant en compte le rapport moléculaire-massique
H2/O de l'eau, nous obtenons une masse d'hydrogène de : X*1/9 kg, soit
dans le meilleur des cas (X=1, c'est à dire que toute l'eau est crackée)
1/9 kg soit 111.11 g d'hydrogène pur par kilogramme d'eau consommée.
Ces
111.11 g d'H2 fournissent une énergie de 13 333 kJ/kg. C'est à dire que
1 kilogramme d'eau fournit au mieux 13 333 kJ, soit l'énergie
équivalente à 13333/36000=0.37 L de fuel.
Il faut donc 2.7 litres d'eau crackée à 100% pour obtenir l'énergie de 1 Litre de fuel.
Remarque importante
: cette dernière affirmation n'est valable que dans le cas d'une
combustion classique d'hydrogène, c'est à dire sans apport d'autre
énergie (quantique ou autre..). De plus comme la combustion de
l'hydrogène forme de l'eau et qu'il est possible de recondenser cette
eau, le "moteur à eau" a la possibilité de "tourner en boucle", les
seules pertes venant de la condensation non parfaite. Cette
recondensation n'est pas effectuée sur les tracteurs mais elle
permettrait de réduire fortement la consommation d'eau.
3.2) Etude de l'énergie fournie par la détente de la (1-X) de la vapeur d'eau.
On considère que sur le même kilogramme d'eau que précédemment,
la portion (1-X) de vapeur d'eau qui n'est pas fractionnée va être
encore être surchauffée et se détendre dans le cylindre pour augmenter
encore la pression sur le piston.
Hypothèse : la vapeur suit
évidement un cycle Diesel, nous calculons l'enthalpie (Energie par
kilogramme) récupérable par cette vapeur injectée. Voici le cycle Diesel
(mixte) dans un diagramme (Pression,Volume). Nous négligeons la boucle
de remplissage et de vidange du moteur.
A)Définition du cycle et des niveaux d'énergie
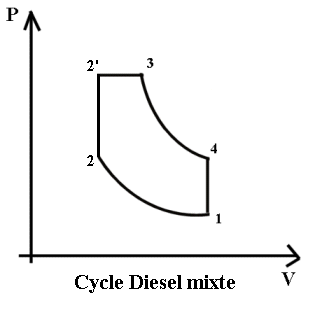 |
Définition du cycle théorique : 1 à 2 : Compression (isentropique) 2 à 2' et 2 à 3 : Combustion(Augmentation de pression et apport de chaleur isobare ) 3 à 4 : Détente (isentropique) = temps moteur 4 à 1 : Vidange = ouverture soupape échappement ( échange de chaleur isochore |
On définit alors les niveaux d'énergie pour les différents points :
Point 1 :
- Température de la vapeur arrivant dans le cylindre : 150°C
- Pression de la vapeur arrivant dans le cylindre : 0.7 bars
- Enthalpie H1 : environ 2800 kJ/kg
Point 2 :
- Température de la vapeur après compression : 400°C
- Pression de la vapeur après compression : 15 bars (taux de compression du moteur Diesel : 20 )
- Enthalpie H2 : environ 3300 kJ/kg
Point 2' (effet de la pression de la combustion):
- Température de la vapeur après compression : 400°C
- Pression de la vapeur après l'explosion : 80 bars
- Enthalpie H2' : environ 3300 kJ/kg
Point 3 (effet de la chaleur de la combustion):
- Température de la vapeur après compression : 1000°C
- Pression de la vapeur après l'explosion : 80 bars
- Enthalpie H3 : environ 5000 kJ/kg
Point 4 :
- Température de la vapeur sortant du moteur : 400°C
- Pression de la vapeur sortant du moteur : 1.5 bars
- Enthalpie H4 : environ 3200 kJ/kg
B) Energies échangées dans le moteur
L'énergie récupérable est l'énergie de détente, c'est à dire
entre le point 3 et le point 4. La compression 1 à 2,au contraire,
demande de l'énergie au moteur.
Energie de compression : H2 - H1 = 500kJ/kg
Energie de combustion : H3 - H2 (ou H2') =1700 kJ/kg ( fournie par le Diesel).
Energie de détente : H3 - H4 = 1800 kJ/kg
L'énergie
récupérable fournie par la vapeur dans le moteur est donc : Energie de
détente - Energie de combustion - Energie de compression = -500 kJ/kg.
D'APRES
NOS HYPOTHESES (températures, pression..), CHAQUE KILOGRAMME DE VAPEUR
D'EAU SORTANT DU REACTEUR ET INJECTEE DANS LE MOTEUR DIESEL VA DONC
FAIRE PERDRE 500 kJ AU CYCLE AU MOTEUR.
Les niveaux d'énergie de l'eau vaporisée en sortie de réacteur et injectée dans le moteur
NE PERMETTENT DONC PAS DE FAIRE GAGNER DE L'ENERGIE AU MOTEUR. AU CONTRAIRE L'EAU VAPEUR POMPE DE LA CHALEUR AU MOTEUR.
POUR RECUPERER L'ENERGIE DE DETENTE DE LA VAPEUR D'EAU, IL
FAUDRAIT UNE VAPEUR D'EAU BIEN PLUS SURCHAUFFEE (plusieurs dizaines de
bars et centaines de degrés) ET INJECTEE EN MEME TEMPS QUE LE FUEL OU
JUSTE APRES L'EXPLOSION. C'est à dire que l'énergie de compression
serait nulle et l'énergie combustion fortement réduite ainsi, l'énergie
récupérable de la détente de la vapeur par le piston bien plus élevée.
3.3) Bilan global de l'énergie fournie par l'eau.
Nous reprenons les notations antérieures : sur 1 kilogramme X %
d'eau est fractionnée, l'énergie fournie par l'hydrogène ou au contraire
pompée par l'eau vapeur est :
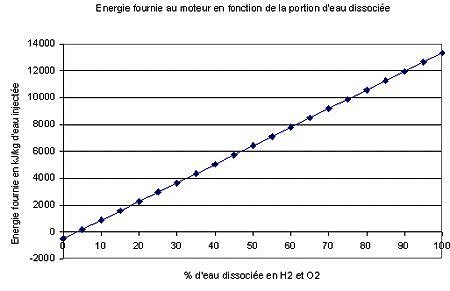
E = Energie fournie par l'hydrogène - Energie pompée par la vapeur = 13333*X - (1-X)*500 = -500 + 13833 X kJ/kg d'eau injectée.
Nous
traçons rapidement le graphique suivant qui donne l'énergie fournie au
moteur par kilogramme d'eau en fonction de la proportion d'eau dissociée
en H2 et O2 (notée X précédemment).